camera transformation

2025-09-01

1. 什么是视图变换？

拍照的过程：
- 先把场景搭好（模型变换）
- 然后找一个角度（视图变换），改变相机的位置，朝那看
- 投影

2. 怎么做视图变换

如何才能确定一个相机的摆放？
- 首先，相机的位置很重要，用位置向量$ \vec{ e }$
- 其次，往哪拍也很重要，用:
  - look-at向量（相机往哪看）：$\hat g$
  - 向上向量（相机头顶的朝向）：$\hat t$
为了简化操作，默认相机在原点$\hat g$是y轴，$\hat t$是-z轴
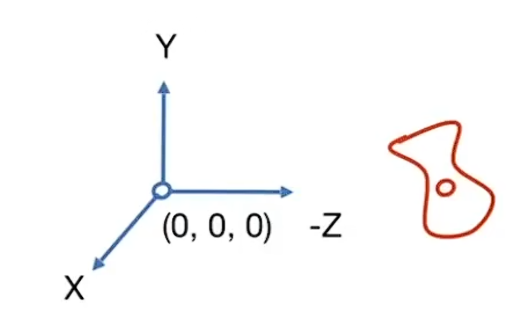
假设相机原始位置为$(x_ e, y_ e, z_ e)$，对他做视图变换：
- 将相机位置平移到原点：$T _ { view } = \begin{bmatrix} 1 &0 &0 &-x_ e \ 0 &1 &0 &-y_e \ 0 &0 &1 &-z_ e \ 0 &0 &0 &1 \end{bmatrix}$
- 将$\hat{ g }$ 旋转到-z轴，将$ \hat t $旋转到y轴，$\hat g \times \hat t$旋转到x轴
  - 直接将$\hat g$旋转到 -z轴不太好操作，旋转矩阵不太好找，可以逆向考虑，考虑先将-z轴根据$R_ { view } ^ { - 1 }$转到$\hat g$，然后由于旋转矩阵的逆矩阵只需要转置就行，求个逆就可以找到旋转矩阵。 $R_ { view } ^ { - 1 } = \begin{bmatrix} x_{ \hat g \times \hat t } &x_ t &x_ { - g } &0 \ y_ { \hat g \times \hat t } &y_t &y_ { -g } &0 \ z_ { \hat g \times \hat t } &z_ t &z_{ -g } &0 \ 0 &0 &0 &1 \end{bmatrix}$
得到$T_ { view }$和$R_ { view }$后，将相机和其他物体都做一个这样的变换

3. 投影

这里的投影并不是指将3D物体映射成2D图片，而是 把相机前的 3D 视见体（view volume）线性/仿射地映射到一个标准的 3D 盒子里（NDC 立方体），而不是立刻产出二维像素图。真正变成 2D 图像是在后面的“透视除法 + 视口映射 + 光栅化”阶段

为什么要先变成立方体（而不是直接二维）？

统一裁剪：无论正交还是透视，先把视见体变成统一的标准盒子（或在齐次裁剪空间的盒状约束），硬件用同一种裁剪逻辑就能处理，效率高。

保留深度：在产出 2D 像素前，需要 zzz 来做隐藏面消除、透明度排序、阴影/雾等效果。

数值/规范化：把范围归一到 [−1,1][-1,1][−1,1]（或 z∈[0,1]z\in[0,1]z∈[0,1]）能简化插值、测试和精度控制。

有两种投影方式：
- 正交投影
- 透视投影
  - 有远小近大

3.1 正交投影

简略理解：
- 经过视图变换之后，只需要将z坐标去掉就行了。
- 然后将结果压缩到$[-1,1] ^2$ （这是一个约定俗称的操作）
正式操作：
- 首先定义空间中的一个立方体：$[l, r] \times [ b, t] \times [f, n]$
- 然后先将立方体的中心移到原点，然后将xyz分别缩放到[-1,1]
  $$
  M_ { ortho } =
  \begin{bmatrix}
  \frac{ 2 }{ r - l } &0 &0 &0 \
  0 &\frac{ 2 }{ t - b } &0 &0 \
  0 &0 &\frac{ 2 }{ n - f } &0 \
  0 &0 &0 &1 \
  \end{bmatrix}
  \begin{bmatrix}
  1 &0 &0 &- \frac{ r+l }{2} \
  0 &1 &0 &- \frac{ t+b }{2} \
  0 &0 &1 &- \frac{ n+f }{2} \
  0 &0 &0 &1
  \end{bmatrix}
  $$

3.2 透视投影

使用最广泛，远小近大，平行线就不再平行了

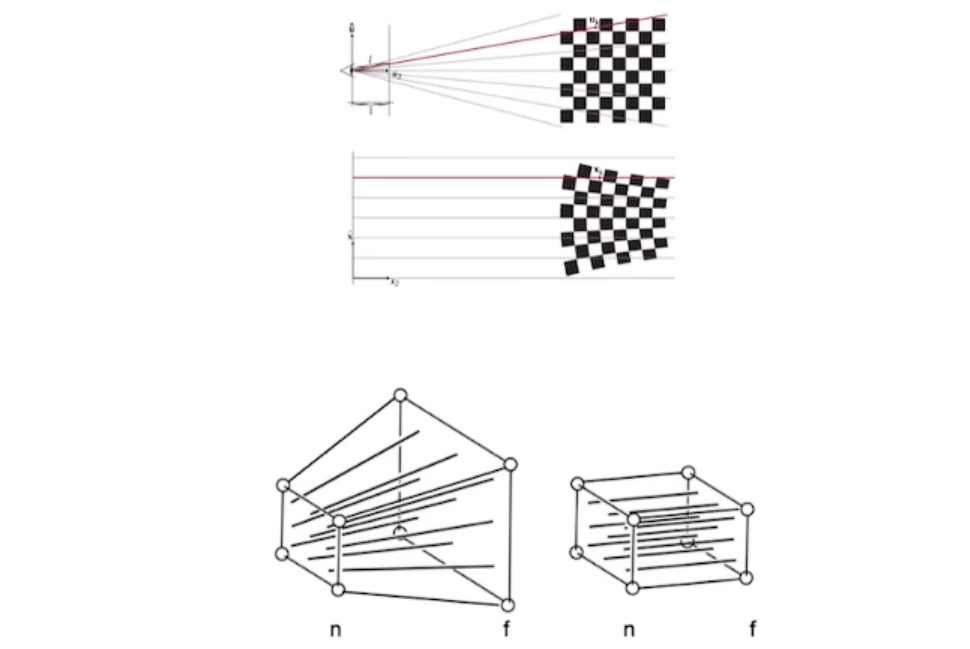
透视投影通过一个视锥观察物体，假设近平面是n，远平面式f，如上图（下），透视投影要做的就是将线的右端点投影到左端点，透视投影跟正交投影的区别就是远平面要大些。

3.2.1 透视投影过程：

假设对远平面进行压缩，把他压缩成跟近平面一样大，（图下从左到右的过程），然后将远平面的点通过正交投影就可以投影到近平面。相当于将透视投影拆分成两个过程：
1. 压缩平面，将远平面到近平面这里所有的平面都压缩成跟近平面一样大
2. 对压缩后得到的立方体做正交投影

1）压缩平面

几个规定假设：
- 近平面压缩后不变（例如顶点压缩后还是原来的顶点，中点压缩后还是原来的中点）
- 远平面压缩后z值不会变化
- 远平面的中心点压缩后不变

对于视锥上的一条线，他在某平面（不一定是远平面）上的点为(x，y，z)，近平面上的点为（x’，y’，z’）这个点压缩后（视锥压缩成立方体），会被压缩成（x‘，y’，z’’），且根据三角形相似可知：$y’ = \frac{ n }{ z} y $ $x’ = \frac{ n }{ z } x$。对于某平面（不一定是远平面）任意一点$ (x, y,z ,1 )^ T$ 会被压缩成$( \frac{ nx }{ z }, \frac{ ny }{ z } , unknown , 1 )$ :
$$
\left ( \begin{matrix} n&0 &0 &0 \
0 &n &0 &0 \ ? &? &? &? \
0 &0 &1 &0
\end{matrix} \right) \times \left ( \begin{matrix} x \
y \ z \
1
\end{matrix} \right) = \left ( \begin{matrix} nx \
ny \ ? \
z
\end{matrix} \right) =\left ( \begin{matrix} \frac{ nx }{ z } \
\frac{ ny }{ z } \ ? \
1
\end{matrix} \right)
$$
- $M_ { persp \rightarrow ortho } = \left ( \begin{matrix} n&0 &0 &0 \
  0 &n &0 &0 \ ? &? &? &? \
  0 &0 &1 &0
  \end{matrix} \right) $
对于近平面上的点，压缩后不变：
$$
\left ( \begin{matrix} n&0 &0 &0 \
0 &n &0 &0 \ 0 &0 &A &B \
0 &0 &1 &0
\end{matrix} \right) \times \left ( \begin{matrix} x \
y \ n \
1
\end{matrix} \right) = \left ( \begin{matrix} nx \
ny \ n^ 2 \
n
\end{matrix} \right) =\left ( \begin{matrix} \frac{ nx }{ n } \
\frac{ ny }{ n } \ n \
1
\end{matrix} \right) \ An+B=n^2
$$
远平面的中心点压缩后不变：$Af + B = f^ 2$
根据$\left { \begin{matrix} An+B=n^2 \ Af + B = f^ 2 \\end{matrix}\right.$ 得：
$$
M_ { persp \rightarrow ortho } = \left ( \begin{matrix} n&0 &0 &0 \
0 &n &0 &0 \ 0 &0 &n+f &-nf \
0 &0 &1 &0
\end{matrix} \right)
$$
最后$M_ { persp } = M_ { orhto } M _ { persp \rightarrow ortho}$